[자료구조] 스택2개를 사용하여 트리를 후위 순회하자!!(작성중)

이번 글에서는 스택 2개를 활용한 후위순회에 관해서 다뤄 보자.

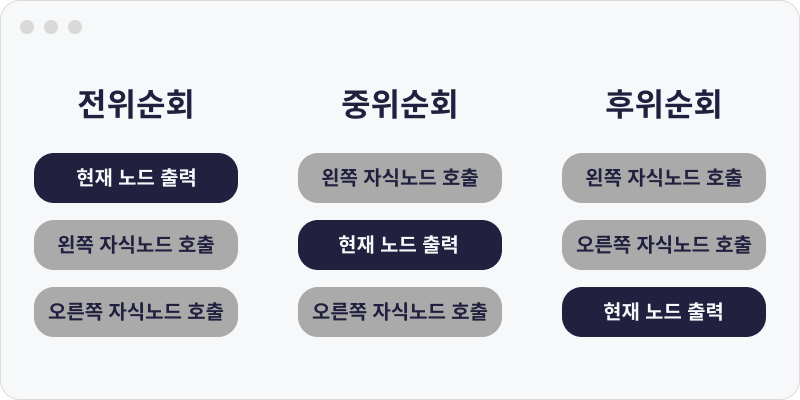
전위, 중위, 후위 순회란?

각각의 공통점은 모두 이진 트리를 탐색하는 방법이라는 거다. 차이는 각 노드를 방문하는 순서에서 나타난다.

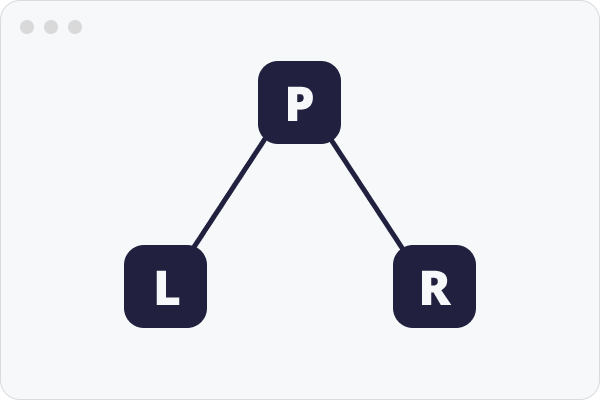
위의 그림은 깊이가 1인 이진 트리이다.

전위 순회

부모 -> 왼쪽 자식 -> 오른쪽 자식
P -> L -> R

중위 순회

왼쪽 자식 -> 부모 -> 오른쪽 자식
L -> P -> R

후위 순회

왼쪽 자식 -> 오른쪽 자식 -> 부모
L -> R -> P

각 각 해당 순서대로 노드를 방문한다.

왼쪽 자식부터 방문 하고 오른쪽 자식을 방문하는 데 부모노드를 언제 방문하냐를 생각하면 이해하기 수월하다.

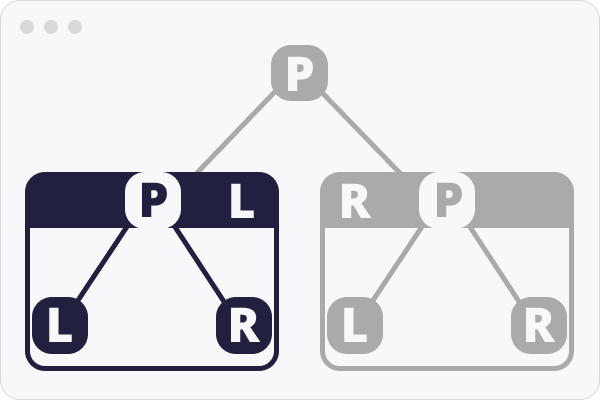
그렇다면 깊이가 2 이상이면 어떻게 될까?

위의 그림은 루트노드의 왼쪽 자식과 그 노드를 부모로 삼는 자식 노드들이 포커스 되어있다.

(굉장히 이미지를 잘 만들어서 이해하기 쉽겠지만) 글로 사진을 설명해보자면 해당 노드를 방문 하면 그 노드를 부모 노드로 생각하며 똑 같은 과정을 진행한다.

언제까지? 노드를 방문하는 노드에 자식노드가 없을 때 까지.

부모 자식으로 이루어진 깊이가 1인 이진 트리를 하나의 노드로 생각하며 그 부모를 방문시 펼쳐진다고 생각하면 좋을 것 같다.

적어도 나는 이렇게 생각했다.

아직은 잘 이해되지 않을 수도 있다. 하지만 코드를 보면서 재귀로 어떻게 트리를 순회하는 지 그려보면 이해가 조금 더 잘 될 수 있다.

사실 재귀를 이용해서 트리를 순회하면 굉장히 직관적이고 (어쩌면?)쉽다.

재귀를 이용한 트리 순회

아래는 방문하는 노드들을 순서대로 출력하는 코드들이다.

일단 하나만 명심하자. 출력함수를 만났다는 것은 방문을 했다는 뜻이다.

전위순회(preorder)

class TreeNode:
    def __init__(self, item):
        self.item = item
        self.left = None
        self.right = None

def preorder(node):
    if node is None:
        return
    print(node.item)
    preOrder(node.left)
    preOrder(node.right)

typedef struct _treeNode {
  int item;
  struct _treeNode* left;
  struct _treeNode* right;
} TreeNode

void preorder(TreeNode *node){
  if (node == NULL) return;
  printf("%d ", node->item);
  preorder(node->left);
  preorder(node->right);
}

중위순회(inorder)

class TreeNode:
    def __init__(self, item):
        self.item = item
        self.left = None
        self.right = None

def inorder(node):
    if node is None:
        return
    inOrder(node.left)
    print(node.item)
    inOrder(node.right)

typedef struct _treeNode {
  int item;
  struct _treeNode* left;
  struct _treeNode* right;
} TreeNode

void inorder(TreeNode *node){
  if (node == NULL) return;
  inorder(node->left);
  printf("%d ", node->item);
  inorder(node->right);
}

후위순회(postorder)

class TreeNode:
    def __init__(self, item):
        self.item = item
        self.left = None
        self.right = None

def postorder(node):
    if node is None:
        return
    postOrder(node.left)
    postOrder(node.right)
    print(node.item)

typedef struct _treeNode {
  int item;
  struct _treeNode* left;
  struct _treeNode* right;
} TreeNode

void postorder(TreeNode *node){
  if (node == NULL) return;
  postorder(node->left);
  postorder(node->right);
  printf("%d ", node->item);
}

코드를 이해 못 한 사람들을 위해 그림을 하나 준비했다.

그림으로 보는 재귀흐름

재귀에 익숙하지 않은 사람들은 이전에 보여준 그림을 한 번 더 참고하자.

두 그림을 같이 보면서 이해하면 쉽다.

첫 번째 그림에서 호출이 일어나면 두 번째 그림과 같이 다음 노드로 만들어진 깊이가 1인 트리를 바라본다. 연속적으로 비슷 한 사건이 발생한다. 그러다 자식이 없는 노드가 호출되면 바라보는 것을 멈추고 다음 단계로 넘어간다. 연속적인 호출이 멈추고(더 이상 자식이 없을 때) 다음 단계의 함수가 실행되고 그 함수가 출력함수면 현재 방문한 노드를 출력하게 된다.

예시로 중위 순회를 들어보겠다.

가장 먼저 왼쪽 자식을 호출한다. 호출하는 순간에는 어떠한 출력도 일어나지 않는다. 왼쪽 노드를 바라봤는데 바라본 노드에도 왼쪽 자식이 있다면 다시 왼쪽 자식을 바라본다.(루트 노드의 손자 노드이다.)

이런 방식을 연속적으로 진행하다가 왼쪽 자식이 없는 순간을 만나면 그 다음 단계인 출력함수가 실행돼서 가장 하위 레벨(리프노드)에 있는 왼쪽노드를 출력하게 되는 것이다. 그 후에 오른쪽 노드로 이루어진 트리들이 같은 방식으로 출력된다.

이제 스택으로 트리를 순회할 준비는 끝났다

반복문과 스택으로 트리 순회

먼저 스택이라는 자료구조에 대해 간단하게 설명하자면 스택은 LIFO(Last In First Out)구조로 되어있다. 가장 늦게 들어간 데이터가 가장 먼저 나온다는 뜻 이다. 스택은 push를 이용하여 데이터를 넣고 pop을 통해 데이터를 꺼낸다. 물론 꺼내온 데이터를 활용할 수도 있다.

여기서 부턴 C언어 코드만 사용한다는 점을 양해 바란다.

스택 1개를 이용한 전위 순회(사전지식)

스택 2개로 후위 순회를 해보자.

앞서 봤듯이 스택을 이용해서 후위 순회를 구현하는 것은 상당히 복잡하고 많은 조건문들이 함께 한다.

그런데 말이다. 꼭 스택을 하나만 사용하라는 법이 있을까?

물론 스택개수가 늘어나면 메모리를 많이 사용하긴 할 것이다.

그치만 메모리보다 내 머리가 먼저 넘쳐 흐를 거 같기 때문에 조금 더 단순한 스택 두 개를 사용한 후위 순회에 대해서 알아보자.

스택에 대한 고찰 잠깐

스택이라는 자료구조에 보통 익숙할 것이다. 개인적으로 스택을 사용할 때 조금은 껄끄러운 것이 있었다. 데이터가 쌓이고 빠져나가는 흐름내에서 스택의 변화는 자연스럽게 머릿속에 그려질 것이다. 하지만 빈 스택에 처음 푸쉬하는 데이터에 대해서는 조금 사고를 일반화 할 필요를 느꼈다.

물론 내 사고가 많이 유연하지 않아서 혼자만 이렇게 생각한 것일 수도 있다..

사실 코드를 보면 쉽게 이해될 때도 많지만 빈 스택인 상태에서 데이터를 쌓고 이것을 사용여 직접 흐름을 만드는 과정은 생각보다 껄끄러웠다.

스택2개를 사용한 후위순회를 하는 과정에서 크게 느꼈다. 물론 나는 이 방법을 공부해서 알고 있었지만 직접 이러한 흐름을 만드는 것은 쉽게 못 할 거 같았다.

트리순회에서 우리에게 처음 주어지는 노드는 루트노드 밖에 없다. 그렇다는 것은 당연하게도 루트노드를 기준으로 사고가 확장 될 것이다.(나는 그렇다.)

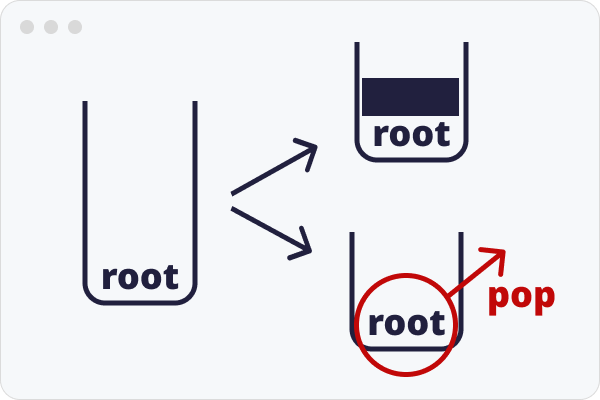
처음 루트노드를 스택에 푸쉬했을 때의 상태에서 생각해보자.

이 때 스택에 푸쉬된 루트노드를 어떻게 정의 할 수 있을까?

일단 가장 먼저 푸쉬 되었으니까, 먼저 푸쉬된 노드?

동시에 마지막에 푸쉬된 노드라고도 생각 할 수 있지 않은가?

아직은 두 가지의 상태가 모두 가능하다.

해당 노드의 속성이 정의 되는 것은 다음 사건에 의해서다. (일종의 슈뢰딩거의 고양이 같은 거다.)

보이는 그림과 같이 스택에 처음 쌓인 데이터에 대하여 위에 다른 데이터가 쌓인다면 먼저 쌓였었다고 정의하고 무엇인가 쌓이지 않고 바로 팝이 된다면 나중에 쌓였었다고 정의할 수 있을 것 같다.

이렇게 정의하고 나면 반복문이 도는 동안 부모노드로 취급되는 모든 노드에 대해서도 같은 정의를 내릴 수 있게된다.

“쓰고보니 당연한 말이지만 이렇게 사고를 일반화 해놓으면 유연하게 사고할 수 있을 거 같단 생각이 들었다.”

물론 나의 경험에 한정해서 서술한 것이다.

본론으로 들어가서..

두개의 스택에 대해서 정의해 보자.

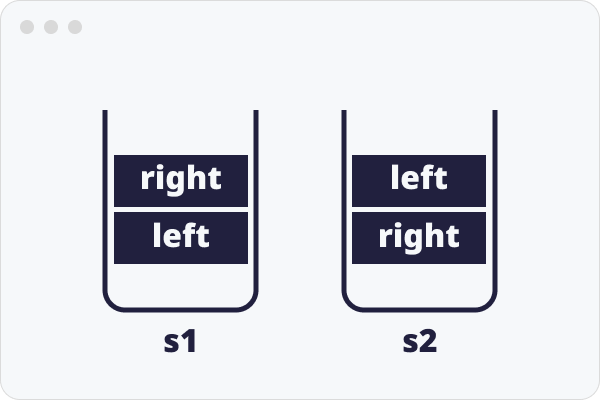
편의상 첫 번째 스택은 s1, 두 번째 스택은 s2로 칭하겠다. s1은 탐색용(중간 저장용)스택, s2는 결과 저장용(출력용)스택이라 정의 할 수 있다.

코드를 보면서 함께 이해해 보자.

void postorder(TreeNode* root){
  if (root == NULL) return;

  Stack* s1 = malloc(sizeof(Stack));
  Stack* s2 = malloc(sizeof(Stack));

  push(s1, root)
}

먼저 스택 2개를 선언하고 s1에 루트 노드를 푸쉬해준다.

이러면 루트 노드를 담은 탐색용 스택 하나와, 아직은 비어 있는 결과 저장용 스택 하나가 준비됐다.

루트노드가 스택에 담겼다. 그럼 앞서 말한 것 처럼 다음 흐름을 보면서 이 처음 스택에 담긴 노드가 어떻게 정의가 되는 지 살펴보자.

void postorder(TreeNode* root){

    //

    while (!isStackEmpty(s1)) {
        TreeNode* node = pop(s1);
        push(s2, node);

        if (node->left) push(s1, node->left);
        if (node->right) push(s1, node->right);
    }
}

s1에 다른 노드가 쌓이는 과정 없이 바로 pop이 된다. 그렇다면 s1에서 루트 노드는 마지막에 쌓인 (쌓였던) 노드로 정의된다.

그런데 잠깐?

어디서 많이 본 듯한 익숙한 코드 아닌가?

위에서 본 전위 순회를 하던 방법과 크게 다르지 않다.

무슨 차이가 있는 지 살펴보자.

일단 전위 순회 시 노드를 출력하는 부분이 결과를 저장용 스택 s2에 노드를 푸쉬하는 것으로 바뀌었다.

우리의 루트 노드는 또 다른 스택에 담겼다. 그럼 다음 코드흐름을 살펴보자.

해당 반복문 내에서 루트 노드 위에 또 다른 노드들이 쌓이고 있다. 그럼 s1에서 가장 마지막에 쌓인 노드 였던 루트노드는 s2라는 스택에서는 가장 먼저 쌓인 노드로 정의되게 된다.

끝인가?

아니다.

비슷 해보이긴 하지만 자식을 스택에 푸쉬하는 부분이 바뀌었다.

위에서 말했듯이 스택은 먼저 나와야할 노드를 나중에 넣어야 한다.

그렇다면 이번에는 오른쪽 노드부터 푸쉬 해야 한다는 것이다.

이 과정을 다시 한 번 정리해보자.

우리는 두개의 스택을 사용한다.

우리는 기본적으로 어떠한 순회를 하던지 왼쪽노드부터 만나게 된다.

그렇다는 것은 결과물을 출력할 노드, s2에 왼쪽노드를 나중에 넣어야 하는 것이다.

스택을 두번 사용하기에 s1에 왼쪽 노드는 먼저 들어가서 나중에 나온다.

나중에 나온 왼쪽 노드는

        push(s2, node);

이 부분에서 나중에 들어가게 된다.

푸쉬된 노드는 그 노드의 자식 노드로 이루어진 트리에서 루트노드로 취급된다.

이제 앞으로의 일이 예상되지 않나??

다음 코드를 확인해보자.

void postorder(TreeNode* root){

    while (!isStackEmpty(s2)) {
        TreeNode* node = pop(s2);
        printf("%d ", node->item);
    }

}

앞선 반복문에서 s2에 넣은 노드들을 팝해주고 있다. 나중에 들어간 왼쪽 노드는 먼저 나오게 된다.

그렇다면 우리의 루트 노드의 여정은 어떻게 될 거 같나?

s2에서 먼저 들어간 루트 노드는 가장 늦게 나오게 된다.

루트 노드로 취급되는 상위노드의 자식노드들도 똑같이 취급된다. 왜냐하면 스택에 먼저 들어갔기 때문이다.

전위 순회를 이해 했다면 이해하기 크게 어렵지 않을 것이다.

void postorder(TreeNode* root){

    //

  free(s1);
  free(s2);
}

우리가 사용한 공간을 깨끗히 비워주자.

한마디로 스택 2개를 이용한 방법은 직관적으로 전위순회를 상하좌우 반전시키는 것과같다.

정리 : 자식 노드 탐색 후 부모노드 탐색, 이를 위해 부모 노드를 다른 스택에 넣어 나중에 꺼내지만 이 과정에서 자녀의 탐색 순서가 서로 바뀌니 처음 스택에 넣을 때 둘을 바꿔준다.

결론 : 재귀가 아주 나쁜 친구인 것 만은 아니다.